Угол правильного многоугольника А₁А₂...А_n равен 135°. Найдите площадь треугольника А₁А₄А₅, если А₁А₅ = 40 ⁴√2.

  Решение:

  1) ((n − 2) · 180°)/n = 135°; 180n − 360 = 135n; 45n = 360, n = 8, значит, дан правильный восьмиугольник (см. рисунок).

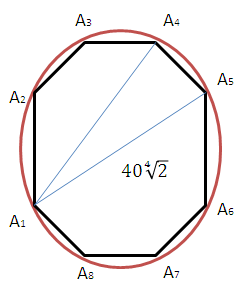
  2) Угол А₁А₅А₄ = углу А₁А₅А₆ (как углы, опирающиеся на равные дуги А₁А₂А₄ и А₁А₈А₆). Следовательно, угол А₁А₅А₄ = 1/2 · угла А₅ = 1/2 · 135° = 67,5°.

  3) Из четырехугольника А₁А₂А₃А₄ следует:

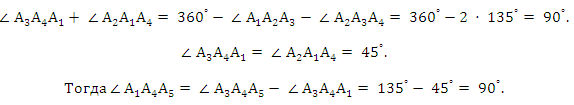
  Следовательно, А₁А₅ - диагональ описанной окружности.

  Сторона восьмиугольника a₈ = 2Rsin(180°/8), где

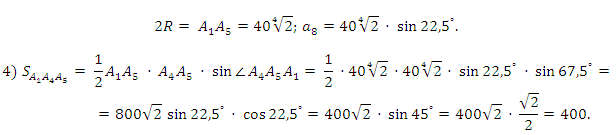
  Ответ: 400.