Точка О есть центр правильного двенадцатиугольника А₁А₂...А₁₂, площадь треугольника А₁А₇А₉ равна 6√3. Найдите площадь А₆ОА₉.

  Решение:

  Так как двенадцатиугольник правильный, то угол А₆ОА₉ равен 3 · 360°/12 = 90° (см. рисунок).

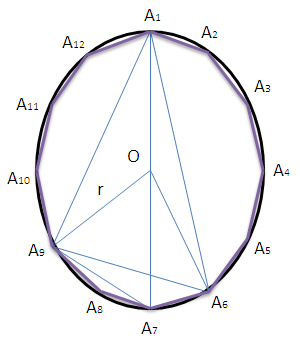
  Обозначим через r радиус, описанной около двенадцатиугольника окружности. Тогда площадь треугольника

S_6ΔA6OA9 = 1/2 · A₆O · A₉O = 1/2 · r².

S_ΔA1OA9 = 1/2 · A₁O · A₉O · sin120° = 1/2 · r²√3/2 = √3 · r²/4;

S_ΔA7OA9 = 1/2 · A₇O · A₉O · sin60° = 1/2 · r² · √3/2 = √3 · r²/4.

  Откуда

S_ΔA1A7A9 = S_ΔA1OA9 + S_ΔA7OA9 = √3 · r²/2 = 6√3.

  Следовательно, r² = 12 => S_ΔA6OA9 = 6.

  Ответ: 6.