Прямоугольная трапеция описана около окружности. Точка касания делит боковую сторону трапеции на отрезки длиной 2 и 8. Найдите периметр трапеции.

  Дано: ABCD - прямоугольная трапеция (см. рисунок), СК = 2, KD = 8, угол BAD = 90°.

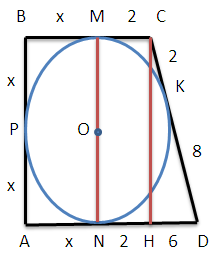
  Найти: P_ABCD.

  Решение:

  Проведем MN перпендикулярно AD через центр вписанной окружности. Тогда точки М и N являются точками касания окружности со сторонами ВС и AD соответственно. МС = СК = 2 и DK = DN = 8 как отрезки касательных.

  ВМ = ВР = РА = AN = х (аналогично). Опустим высоту СН.

  HD = DN − NH = 8 − 2 = 6. Из треугольника HCD: CH² = 10² − 6² = 8²; CH = 8.

  BA и СН - параллельны, так как по условию угол BAD = 90°. Следовательно, ВА = СН (как отрезки, заключенные между параллельными прямыми). Получаем: 2х = 8; х = 4.

  Теперь найдем P_ABCD = 4х + 2 + 10 + 8 = 20 + 16 = 36.

  Ответ: 36.