В параллелограмме ABCD биссектрисы углов В и С пересекают сторону AD в точках К и L соответственно. Найдите площадь параллелограмма ABCD, если известно, что BL = 6, СК = 8 и АВ : AD = 1 : 3.

  Решение:

  1) Так как углы АВL, CBL и BLA - равны, то АВ = AL.  Аналогично CD = CK. Следовательно, учитывая условие, получаем:

LK = AD − AL − DK = 3AB − 2AB = AB (см. рисунок).

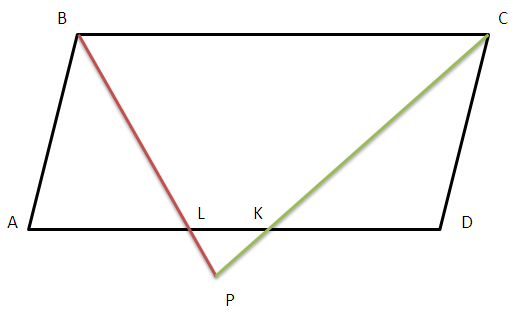
  Пусть Р - точка пересечения прямых BL и СК. Так как LK и ВС - параллельны, то треугольник LKP и треугольник ВСР - подобны с коэффициентом подобия k = LK/BC = 1/3.

  Имеем: PL = BP/3, BL = 2BP/3, BP = 3BL/2 = 9.

  Аналогично находим, что СР = 3СК/2 = 12.

  2) Так как угол РВС равен половине угла В, угол РСВ равен половине угла С, а сумма углов РВС и РСВ равна половине суммы углов В и С (т.е. 90°), то угол ВРС = 90°.

  3) S_BCP = BP/2 · CP = 54, S_LKP = k² · S_BPC = 1/9 · 54 = 6.

  Итак, S_BCKL = S_BCP − S_LKP = 48,

  S_BCKL = h/2 · (BC + LK) = h/2 · 4BC/3 = 2/3 · S_ABCD (h - высота параллелограмма).

  Следовательно, S_ABCD = 3/2 · S_BCKL = 72.

  Ответ: 72.