31 декабря 2014 года Сергей взял в банке 6944000 рублей в кредит под 12,5% годовых. Схема выплаты кредита следующая - 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 12,5%), затем Сергей переводит в банк Х рублей. Какой должна быть сумма Х, чтобы Сергей выплатил долг тремя равными платежами (то есть за три года)?

  Решение:

  Пусть сумма кредита равна S, а годовые составляют а%. Тогда 31 декабря каждого года оставшаяся сумма долга умножается на коэффициент b = 1 + 0,01a. После первой выплаты сумма долга составит S₁ = Sb − X. После второй выплаты сумма долга составит

S₂ = S₁b − X = (Sb − X)b − X = Sb² − (1 + b)X.

  После третьей выплаты сумма оставшегося долга равна

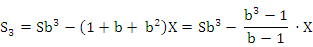
  По условию задачи с учетом третьей выплаты Сергей должен погасить кредит полностью, поэтому

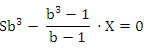
откуда получаем

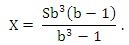
  При S = 6944000 и а = 12,5, получаем:

b = 1,125

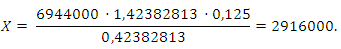
  Ответ: 2916000.

  пример включения этой задачи в тест ЕГЭ