Дан правильный шестиугольник А₁А₂А₃А₄А₅А₆. В₁, В₂, В₃, В₄, В₅, В₆ - середины сторон А₁А₂, А₂А₃, А₃А₄, А₄А₅, А₅А₆, А₆А₁ соответственно. Найдите отношение площади В₁В₂В₃В₄В₅В₆ к площади А₁А₂А₃А₆.

  Решение:

  Пусть А₁А₂ = а, а > 0, тогда так как треугольник ОА₁А₂ - равносторонний, то ОВ₁ = а√3/2 (см. рисунок).

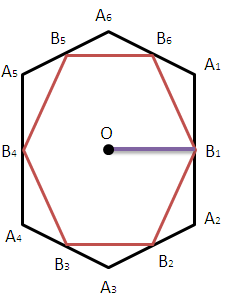
  S_A1A2A3A6 = 3 · S_A1OA2 = 3 · (a²√3)/4;

  S_B1B2B3B4B5B6 = 6 · 1/2 · S_B1OB2 = 3 · OB₁ · OB₂sinB₁OB₂ = 3 · a√3/2 · a√3/2 · sin60° = 9a²√3/8;

  S_B1B2B3B4B5B6 / S_A1A2A3A6 = (9 · a²√3/8) / (3 · a²√3/4) = 1,5.

  Ответ: 1,5.