Хорды АС и BD окружности перпендикулярны и пересекаются в точке Р. РН - высота в треугольнике ADP. Угол ADP = 30°, АН = 2, РС = 6. Найдите отношение площади треугольника ADC к площади треугольника АВС.

  Решение:

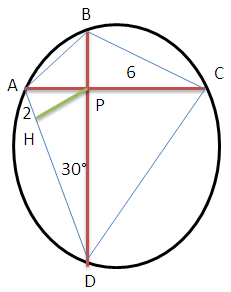
  Углы АРН и ADP равны (см. рисунок), так как каждый из них в сумме с углом РАН дает 90°. Следовательно, угол АРН = 30°. АР = АН/sin30° = 4. PD = AP · ctg30° = 4√3. Углы DAC и DBC равны как опирающиеся на одну дугу. Углы ВРС и APD - равны (как вертикальные). Следовательно, треугольники ADP и ВСР подобны.

  AP : PD = BP : PC

BP = (AP · PC)/DP = 2√3

S_ADC / S_ABC = (1/2 · DP · AC) / (1/2 · PB · AC) = DP/BP = 2

  Ответ: 2.