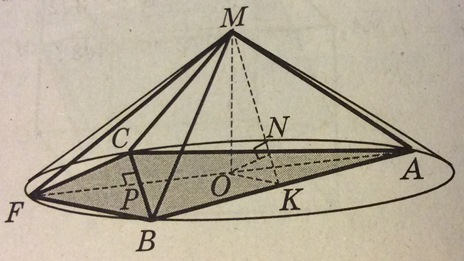
Дан конус с вершиной М, радиус основания которого равен 6. На окружности его основания выбраны точки А, В, С так, что углы ВМА, АМС, СМВ равны 90^° каждый. Точка F выбрана на дуге ВС окружности основания конуса, не содержащей точки А, так, что объем пирамиды МАВFC наибольший. Найдите расстояние от точки F до плоскости МАВ.

 

  Решение:

  Прежде всего, неплохо было бы определить местоположение точки F: если все остальные вершины пирамиды фиксированы, то ее объем максимален, когда эта точка на окружности наиболее удалена от хорды ВС.

  Далее, исходная пирамида - конечно, правильная, и она полностью задана. Значит, остальное - дело техники (точнее, арифметики).

 

 

 

  1. Объем V_MABFC - максимален, когда F - середина дуги ВС, т.к. :

  а) V_MABFC = ¹/₃ · MO · (S_ABC + S_BCF) = ¹/₃ · MO · (S_ABC + ¹/₂ · BC · FP);

  б) высота FP - максимальна, когда FP - серединный перпендикуляр к хорде ВС.

 

  2. Δ АМВ = Δ АМС = Δ СМВ (т.к. МА = МВ = МС и углы АМВ, АМС и СМВ - равны 90^° каждый) => Δ ABC - правильный.

 

  3. К - середина АВ (=> Δ АОК - прямоугольный):

  а) ОК = АО · sin 30^° = 6/2 = 3;

  б) АВ = 2АК = 2 · АО · cos 30^° = 6√3.

 

  4. ON перпендикулярен МК:

  ОК, МК - перпендикулярны АВ => ON - перпендикулярен АВМ.

 

  5. FH - перпендикуляр к плоскости АВМ:

  FH : ON = FA : OA (Δ AFH подобен Δ AON) = 2 : 1, т.к. FA - диаметр, ОА - радиус.

 

  6. Δ АВМ, Δ АМО, Δ ОКМ - прямоугольные:

 

 

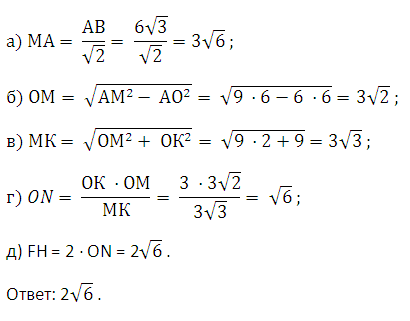
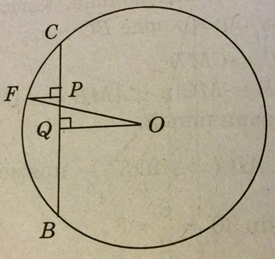
  В нашем решении голословно заявлено, что высота FP - максимальна, когда FP - серединный перпендикуляр к хорде ВС. Можно ли обосновать этот факт? Да, например, с помощью следующих двух соображений:

  1) если OQ - серединный перпендикуляр к хорде ВС, то справедлива оценка

FP + OQ ≤ OF <=> FP ≤ OF - OQ (=const),

 

 

  2) равенство в полученной оценке достигается тогда и только тогда, когда

P,Q принадлежат OF <=> OF перпендикулярен ВС.