ТЕСТ ЕГЭ - 2015 ПО МАТЕМАТИКЕ
ПРОФИЛЬНЫЙ УРОВЕНЬ
ВАРИАНТ 3
ЧАСТЬ 1
1. В розницу один номер еженедельного журнала "Репортаж" стоит 26 руб., а полугодовая подписка на этот журнал стоит 590 руб. За полгода выходит 25 номеров журнала. Сколько рублей сэкономит г-н Иванов за полгода, если не будет покупать каждый номер журнала отдельно, а оформит подписку?
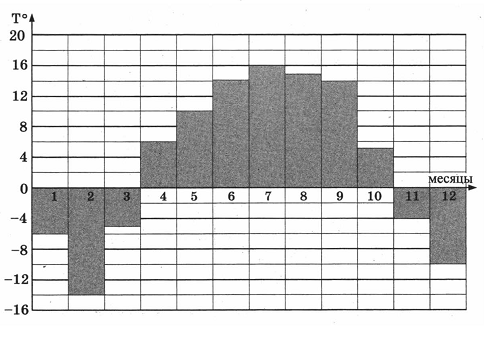
2. На диаграмме показана средняя температура воздуха в Нижнем Новгороде за каждый месяц 1994 года. По горизонтали указываются месяцы, по вертикали - средняя температура в градусах Цельсия. Определите по диаграмме, сколько было месяцев с отрицательной средней температурой в 1994 году в Нижнем Новгороде.
3. В трёх салонах сотовой связи один и тот же телефон продаётся в кредит на разных условиях. Условия даны в таблице.
| Салон |
Цена телефона, руб. |
Первоначальный взнос, в процентах от цены |
Срок кредита, мес. |
Сумма ежемсячного платежа, руб. |
| Эпсилон | 11900 | 15 | 12 | 910 |
| Дельта | 12000 | 30 | 12 | 770 |
| Омикрон | 12200 | 20 | 6 | 1700 |
Определите, в каком из салонов покупка обойдётся дороже всего (с учётом переплаты), и в ответ напишите эту наибольшую сумму в рублях.
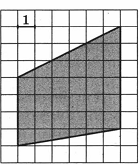
4. Найдите площадь трапеции, изображённой на клетчатой бумаге с размером клетки 1 см х 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
5. В случайном эксперименте симметричную монету бросают четырежды. Найдите вероятность того, что орёл выпадет ровно три раза.
6. Найдите корень уравнения
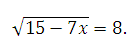
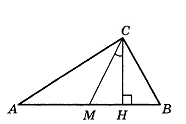
7. В прямоугольном треугольнике угол между высотой и медианой, проведёнными из вершины прямого угла, равен 28°. Найдите больший из острых углов этого треугольника. Ответ дайте в градусах.
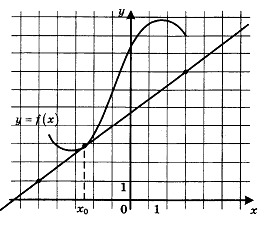
8. На рисунке изображены график функции y = f(x) и касательная к нему в точке с абсциссой х0. Найдите значение производной функции f(x) в точке х0.
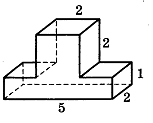
9. Найдите объём многогранника, изображённого на рисунке (все двугранные углы прямые).
ЧАСТЬ 2
10. Найдите значение выражения
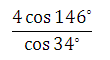
11. Для определения эффективной температуры звёзд используют закон Стефана-Больцмана, согласно которому мощность излучения нагретого тела Р, измеряемая в ваттах, прямо пропорциональна площади его поверхности и четвёртой степени температуры:
Р = σST4
где σ = 5,7 · 10-8 - постоянная, площадь S измеряется в квадратных метрах, а температура Т - в градусах Кельвина. Известно, что некоторая звезда имеет площадь
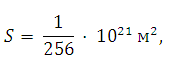
а излучаемая ею мощность Р равна 5,7 · 1025 Вт. Определите температуру этой звезды. Ответ выразите в градусах Кельвина.
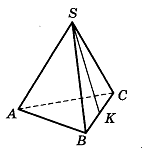
12. В правильной треугольной пирамиде SABC точка К - середина ребра ВС, S - вершина. Известно, что АВ = 6, а длина отрезка SK = 7. Найдите площадь боковой поверхности пирамиды.
13. Из пункта А в пункт В одновременно выехали два автомобиля. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью 50 км/ч, а вторую половину пути - со скоростью, на 15 км/ч большей скорости первого, в результате чего прибыл в В одновременно с первым автомобилем. Найдите скорость первого автомобиля. Ответ дайте в км/ч.
14. Найдите наименьшее значение функции у = х3 + 18х2 + 17 на отрезке [−3; 3].
Для записи решений и ответов на задания 15 - 21 используйте бланк ответов №2. Запишите сначала номер выполняемого задания (15, 16 и т.д.), а затем полное обоснованное решение и ответ. Ответы записывайте чётко и разборчиво.
15. а) Решите уравнение 2sin4x + 3cos2x + 1 = 0.
б) Найдите все корни этого уравнения, принадлежащие отрезку [π; 3п].
16. Площадь боковой поверхности правильной четырёхугольной пирамиды SABCD равна 108, а площадь полной поверхности этой пирамиды равна 144.
а) Постройте прямую пересечения плоскости SAC и плоскости, проходящей через вершину S этой пирамиды, середину стороны АВ и центр основания.
б) Найдите площадь сечения пирамиды плоскостью SAC.
17. Решите неравенство
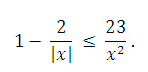
18. Медианы АА1, ВВ1 и СС1 треугольника АВС пересекаются в точке М. Точки А2, В2 и С2 - середины отрезков МА, МВ и МС соответственно.
а) Докажите, что площадь шестиугольника А1В2С1А2В1С2 вдвое меньше площади треугольника АВС.
б) Найдите сумму квадратов всех сторон этого шестиугольника, если известно, что АВ = 5, ВС = 8 и АС = 10.
19. 1 января 2015 года Александр Сергеевич взял в банке 1,1 млн рублей в кредит. Схема выплаты кредита следующая - 1 числа каждого следующего месяца банк начисляет 1 процент на оставшуюся сумму долга (то есть увеличивает долг на 1%), затем Александр Сергеевич переводит в банк платёж. На какое минимальное количество месяцев Александр Сергеевич может взять кредит, чтобы ежемесячные выплаты были не более 275 тыс. рублей?
20. Найдите все значения параметра а, при каждом из которых уравнение
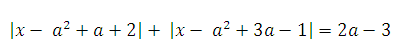
имеет корни, но ни один из них не принадлежит интервалу (4; 19).
21. Возрастающая конечная арифметическая прогрессия состоит из различных целых неотрицательных чисел. Математик вычислил разность между квадратом суммы всех членов прогрессии и суммой их квадратов. Затем математик добавил к этой прогрессии следующий её член и снова вычислил такую же разность.
а) Приведите пример такой прогрессии, если во второй раз разность оказалась на 48 больше, чем в первый раз.
б) Во второй раз разность оказалась на 1440 больше, чем в первый раз. Могла ли прогрессия сначала состоять из 12 членов?
в) Во второй раз разность оказалась на 1440 больше, чем в первый раз. Какое наибольшее количество членов могло быть в прогрессии сначала?


