ТЕСТ ЕГЭ - 2015 ПО МАТЕМАТИКЕ
ПРОФИЛЬНЫЙ УРОВЕНЬ
ВАРИАНТ 2
Часть 1
1. Магазин закупает цветочные горшки по оптовой цене 90 рублей за штуку и продает с наценкой 15%. Какое наибольшее число таких горшков можно купить в этом магазине на 700 рублей?
Ответ
2. На рисунке жирными точками показана среднесуточная температура воздуха в Пскове каждый день с 15 по 28 марта 1959 г. По горизонтали указываются числа месяца, по вертикали - температура в градусах Цельсия. Для наглядности жирные точки соединены линией. Определите по рисунку, какой была наименьшая среднесуточная температура за указанный период. Ответ дайте в градусах Цельсия.
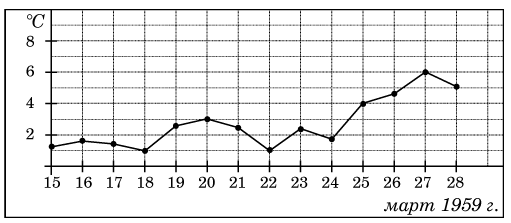
Ответ
3. Интернет-провайдер предлагает три тарифных плана.
| Тарифный план |
Абонентская плата | Плата за трафик |
| План "0" | Нет | 2,5 руб. за 1 Мб |
| План "500" | 550 руб. за 500 Мб трафика в месяц | 2 руб. за 1 Мб сверх 500 Мб |
| План "800" | 700 руб. за 800 Мб трафика в месяц | 1,5 руб. за 1 Мб сверх 800 Мб |
Пользователь предполагает, что его трафик составит 570 Мб в месяц, и исходя из этого выбирает наиболее дешёвый тарифный план. Сколько рублей должен будет заплатить пользователь за месяц, если его трафик действительно будет равен 570 Мб?
Ответ
4. Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см х 1 см. Ответ дайте в квадратных сантиметрах.
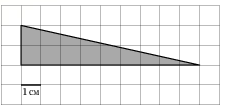
Ответ
5. В случайном эксперименте бросают три игральные кости. Найдите вероятность того, что сумма выпавших очков равна 15. Результат округлите до тысячных.
Ответ
6. Найдите корень уравнения:
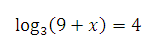
Ответ
7. В треугольнике АВС угол С равен 90°, СН - высота, угол А равен 60°, АВ = 12. Найдите ВН.
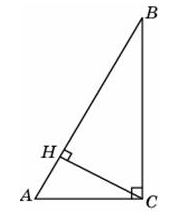
Ответ
8. Прямая у = 4х + 8 параллельна касательной к графику функции
у = х2 − 5х + 7.
Найдите абсциссу точки касания.
Ответ
9. Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 8,5. Найдите объем параллелепипеда.
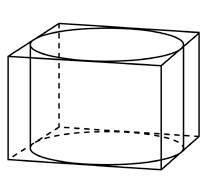
Ответ
Часть 2
10. Найдите значение выражения:
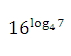
Ответ
11. Зависимость объёма спроса q (единиц в месяц) на продукцию предприятия-монополиста от цены р (тыс. руб.) задаётся формулой
q = 100 − 4p.
Выручка предприятия за месяц r (в тыс. руб.) вычисляется по формуле
r(p) = q · p.
Определите наибольшую цену р, при которой месячная выручка r(p) составит не менее 600 тыс. руб. Ответ приведите в тыс. руб.
Ответ
12. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 3 и 4. Площадь поверхности этого параллелепипеда равна 94. Найдите третье ребро, выходящее из той же вершины.
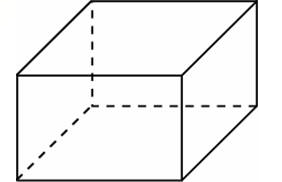
Ответ
13. Из пункта А в пункт В одновременно выехали два автомобиля. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью 42 км/ч, а вторую половину пути - со скоростью, на 28 км/ч большей скорости первого, в результате чего прибыл в пункт В одновременно с первым автомобилем. Найдите скорость первого автомобиля. Ответ дайте в км/ч.
Ответ
14. Найдите наименьшее значение функции
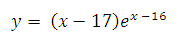
на отрезке [15; 17].
15. Решите уравнение
4cosx ctgx + 4ctgx + sinx = 0.
Ответ
16. Внутри правильного тетраэдра ABCD с ребром, равным 12, расположен конус, вершина которого является серединой ребра CD. Основание конуса вписано в сечение тетраэдра, проходящее через середину ребра ВС параллельно прямым СD и АВ. Найдите объём конуса.
Ответ
17. Решите неравенство
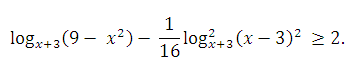
Ответ
18. Две окружности касаются внешним образом в точке К. Прямая касается первой окружности в точке А, а второй - в точке В. Прямая ВК пересекает первую окружность в точке D, прямая АК пересекает вторую окружность в точке С.
а) Докажите, что AD и ВС параллельны.
б) Найдите площадь треугольника DKC, если известно, что радиусы окружностей равны 1 и 14.
Ответ
19. 31 декабря 2012 года Михаил Александрович взял в банке 3200000 рублей в кредит под 16% годовых. Схема выплаты кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 16%), затем Михаил Александрович переводит в банк определенную сумму ежегодного платежа. Какой должна быть сумма ежегодного платежа, чтобы Михаил Александрович выплатил долг тремя равными ежегодными платежами?
Ответ
20. Найдите все значения а, при каждом из которых оба числа
4sina − 3 и 8cos2a + 16sina + 1
являются решениями неравенства
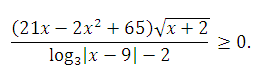
Ответ
21. Найдите все пары натуральных чисел m ≤ n разной четности, удовлетворяющие уравнению
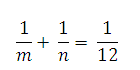
Ответ


