Часть 1

  1. Железнодорожный билет для взрослого стоит 220 рублей. Стоимость билета для школьника составляет 50% от стоимости билета для взрослого. Группа состоит из 16 школьников и 3 взрослых. Сколько рублей стоят билеты на всю группу?

 

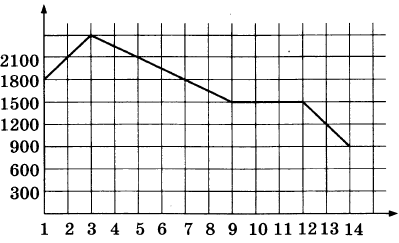
  2. На графике, изображённом на рисунке, представлено изменение биржевой стоимости акций газодобывающей компании в первые две недели ноября. 2 ноября бизнесмен приобрел 10 акций этой компании. Шесть из них он продал 6 ноября, а 13 ноября - остальные 4. Сколько рублей потерял бизнесмен в результате этих операций?

 

 

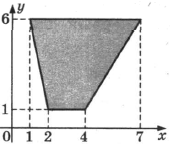
  3. Найдите площадь трапеции, вершинами которой являются точки с координатами (1; 6), (7; 6), (4; 1), (2; 1).

 

 

  4. В среднем из 150 карманных фонариков - три неисправных. Найдите вероятность купить работающий фонарик.

 

  5. Найдите корень уравнения х² − 15 = (х − 15)².

 

  6. Концы отрезка АВ лежат по разные стороны от прямой l. Расстояние от точки А до прямой l равно 7, а расстояние от точки В до прямой l равно 13. Найдите расстояние от середины отрезка АВ до прямой l.

 

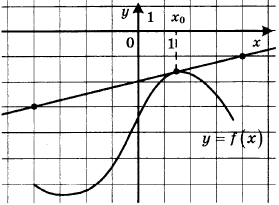
  7. На рисунке изображены график функции у = f(x) и касательная к нему в точке с абсциссой х₀. Найдите значение производной функции f(x) в точке х₀.

 

 

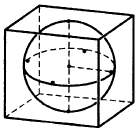
  8. Шар, объём которого равен 14п, вписан в куб. Найдите объём куба.

 

 

Часть 2

  9. Вычислите значение выражения

 

 

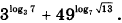
  10. Коэффициент полезного действия (КПД) некоторого двигателя определяется формулой 

 

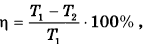
  где Т₁ - температура нагревателя (в градусах Кельвина), Т₂ - температура холодильника (в градусах Кельвина). При какой температуре нагревателя Т₁ КПД двигателя будет 15%, если температура холодильника Т₂ = 340 °К? Ответ выразите в градусах Кельвина.

 

  11. Из пункта А круговой трассы, длина которой равна 30 км, одновременно в одном направлении стартовали два автомобилиста. Скорость первого равна 92 км/ч, скорость второго - 77 км/ч. Через сколько минут первый автомобилист будет опережать второго ровно на 1 круг?

 

  12. Найдите наибольшее значение функции

 

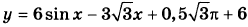
  на отрезке [0; п/2].

 

  13. а) Решите уравнение 6sin²x + 7cos x − 7 = 0.

  б) Найдите все корни этого уравнения, принадлежащие отрезку [−3п; −п].

 

  14. В прямоугольном параллелепипеде ABCDA₁B₁C₁D₁ известны длины рёбер АА₁ = 7, АВ = 16, AD = 6. Точка К - середина ребра C₁D₁.

  а) Докажите, что плоскость, проходящая через точку В перпендикулярно прямой АК, пересекает отрезок А₁К.

  б) Найдите тангенс угла между этой плоскостью и плоскостью АВС.

 

  15. Решите неравенство

 

 

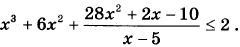
  16. На катетах АС и ВС прямоугольного треугольника АВС вне треугольника построены квадраты ACDE и BFKC. Точка М - середина гипотенузы АВ, Н - точка пересечения прямых СМ и DK. 

  а) Докажите, что СМ перпендикулярно DK.

  б) Найдите МН, если известно, что катеты треугольника АВС равны 130 и 312.

 

  17. 15-го января планируется взять кредит в банке на 18 месяцев. Условия его возврата таковы:

  - 1-го числа каждого месяца долг возрастает на 2% по сравнению с концом предыдущего месяца;

  - со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;

  - 15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца.

  Сколько процентов от суммы кредита составляет общая сумма денег, которую нужно выплатить банку за весь срок кредитования?

 

  18. Найдите все значения а, при каждом из которых уравнение

 

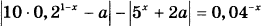
  имеет ровно два неотрицательных решения.

 

  19. Конечная возрастающая последовательность а₁, а₂, ..., а_n состоит из n ≥ 3 не обязательно различных натуральных чисел, причём при всех натуральных k ≤ n − 2 выполнено равенство 

 

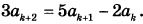
  а) Приведите пример такой последовательности при n = 4.

  б) Может ли в такой последовательности при некотором n ≥ 3 выполняться равенство a_n = 3a₂ − 2a₁?

  в) Какое наименьшее значение может принимать а₁, если a_n = 667?

 

Ответы:

 

 

другие варианты для тренировки