Часть 1
1. Пакет молока стоит 21 рубль 30 копеек. Какое наибольшее количество пакетов молока можно купить на 500 рублей?
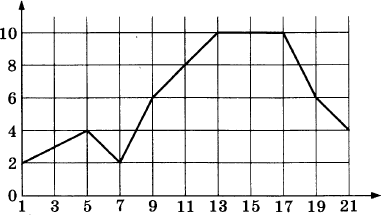
2. Первый посев семян петрушки рекомендуется проводить в апреле при дневной температуре воздуха не менее +6 °С. На рисунке показан прогноз дневной температуры воздуха на первые три недели апреля. Определите, в течение скольких дней за этот период можно производить посев петрушки.
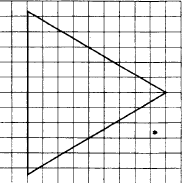
3. На клетчатой бумаге с размером клетки 1 х 1 изображён равносторонний треугольник. Найдите радиус вписанной в него окружности.
4. Перед началом первого тура чемпионата по шашкам участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвуют 56 шашистов, среди которых 12 участников из России, в том числе Валерий Стремянкин. Найдите вероятность того, что в первом туре Валерий Стремянкин будет играть с каким-либо шашистом из России.
5. Найдите корень уравнения 54 − х = 25.
6. Отрезок АВ является хордой окружности с центром О. Найдите угол между прямой АВ и касательной к окружности, проходящей через точку А, если угол АОВ равен 56°. Ответ дайте в градусах.
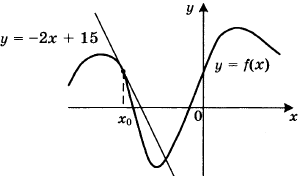
7. На рисунке изображены график функции у = f(х) и касательная к этому графику, проведённая в точке х0. Касательная задана уравнением у = −2х + 15. Найдите значение производной функции
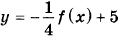
в точке х0.
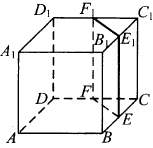
8. В кубе АВСDA1B1C1D1 точки Е, F, E1 и F1 являются серединами рёбер BC, DC, B1C1 и D1C1 соответственно. Объём призмы, отсекаемой от куба плоскостью EFF1, равен 14. Найдите объём куба.
Часть 2
9. Найдите значение выражения (5582 − 232) : 581.
10. Ёмкость высоковольтного конденсатора в телевизоре С = 4 · 10−6 Ф. Параллельно с конденсатором подключён резистор с сопротивлением R = 2 · 106 Ом. Во время работы телевизора напряжение на конденсаторе U0 = 22 кВ. После выключения телевизора напряжение на конденсаторе убывает до значения U (кВ) за время, определяемое выражением
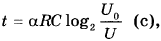
где α = 1,7 с / Ом · Ф - постоянная. Определите напряжение на конденсаторе, если после выключения телевизора прошло 27,2 секунды. Ответ дайте в кВ (киловольтах).
11. В сосуд, содержащий 7 литров 15-процентного водного раствора некоторого вещества, добавили 8 литров воды. Сколько процентов составит концентрация получившегося раствора?
12. Найдите наибольшее значение функции
у = (21 − х)ех − 20
на отрезке [19; 21].
13. Решите уравнение
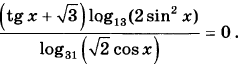
14. В правильной четырёхугольной пирамиде SABCD с вершиной S сторона основания равна 4. Точка L - середина ребра SC. Тангенс угла между прямыми BL и SA равен
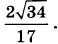
а) Пусть О - центр основания пирамиды. Докажите, что прямые BO и LO перпендикулярны.
б) Найдите площадь поверхности пирамиды.
15. Решите неравенство
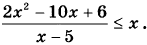
16. Окружность с центром О вписана в угол, равный 60°. Окружность большего радиуса с центром О1 также вписана в этот угол и проходит через точку О.
а) Докажите, что радиус второй окружности вдвое больше радиуса первой.
б) Найдите длину общей хорды этих окружностей, если известно, что радиус первой окружности равен 2√3.
17. В двух областях есть по 90 рабочих, каждый из которых готов трудиться по 5 часов в сутки на добыче алюминия или никеля. В первой области один рабочий за час добывает 0,3 кг алюминия или 0,1 кг никеля. Во второй области для добычи х кг алюминия в день требуется х2 человеко-часов труда, а для добычи у кг никеля в день требуется у2 человеко-часов труда.
Для нужд промышленности можно использовать или алюминий, или никель, причём 1 кг алюминия можно заменить 1 кг никеля. Какую наибольшую массу металлов можно добыть в двух областях суммарно для нужд промышленности?
18. Найдите все значения параметра а, при каждом из которых неравенство
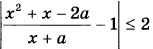
не имеет решений на интервале (1; 2).
19. Решите в целых числах уравнение 3n + 8 = x2.
Ответы:


все варианты тренировочных тестов


