ТЕСТ ЕГЭ - 2017 ПО МАТЕМАТИКЕ
БАЗОВЫЙ УРОВЕНЬ
ВАРИАНТ 5
1. Найдите значение выражения
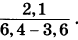
2. Найдите значение выражения
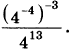
3. Шариковая ручка стоит 30 рублей. Какое наибольшее число таких ручек можно будет купить на 600 рублей после повышения цены на 25%?
4. Найдите m из равенства E = mv2/2, если v = 3 и Е = 54.
5. Найдите значение выражения
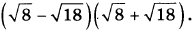
6. В пачке 500 листов бумаги формата А4. За неделю в офисе расходуется 600 листов. Какого наименьшего количества пачек бумаги хватит на 6 недель?
7. Найдите корень уравнения log4(7 + x) = 2.
8. Столб подпирает детскую горку посередине. Найдите высоту l этого столба, если высота h горки равна 4 м. Ответ дайте в метрах.
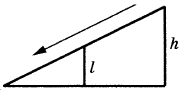
9. Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца.
ВЕЛИЧИНЫ ЗНАЧЕНИЯ
А) результат при прыжке в высоту 1) 520 см
Б) высота полёта самолёта 2) 8 км
В) толщина нити рыболовной сетки 3) 1,8 м
Г) длина стены в комнате 4) 0,3 мм
В таблице под каждой буквой, соответствующей величине, укажите номер её возможного значения.
| А | Б | В | Г |
10. В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орёл выпадет хотя бы один раз.
11. В соревнованиях по метанию молота участники показали следующие результаты:
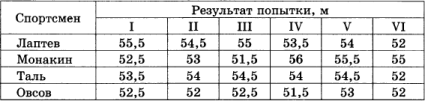
Места распределяются по результатам лучшей попытки каждого спортсмена: чем дальше он метнул молот, тем лучше.
Какое место занял спортсмен Лаптев?
12. Интернет-провайдер предлагает три тарифных плана.

Пользователь предполагает, что его трафик составит 850 Мб в месяц, и исходя из этого выбирает наиболее дешёвый тарифный план. Сколько рублей должен будет заплатить пользователь за месяц, если его трафик действительно будет равен 850 Мб?
13. Пирамида Хеопса имеет форму правильной четырёхугольной пирамиды, сторона основания которой равна 230 м, а высота - 147 м. Сторона основания точной музейной копии этой пирамиды равна 23 см. Найдите высоту музейной копии. Ответ дайте в сантиметрах.
14. На рисунке изображён график функции у = f(х). Точки а, b, c, d и е задают на оси Ох интервалы. Пользуясь графиком, поставьте в соответствие каждому интервалу характеристику функции или её производной.
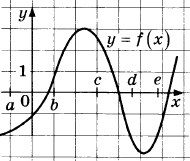

В таблице под каждой буквой укажите соответствующий номер.
| А | Б | В | Г |
15. В треугольнике АВС проведена медиана ВМ, на стороне АВ взята точка К так, что АК = 1/5 · АВ. Площадь треугольника АМК равна 3. Найдите площадь треугольника АВС.
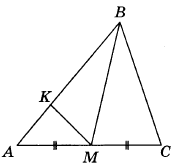
16. В основании пирамиды SABC лежит правильный треугольник АВС со стороной 2, а боковое ребро SA перпендикулярно основанию и равно 5√3. Найдите объём пирамиды SABC.
17. Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями.
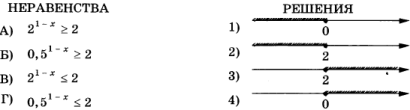
Впишите в приведённую в ответе таблицу под каждой буквой соответствующий решению номер.
| А | Б | В | Г |
18. Двадцать выпускников одного из одиннадцатых классов сдавали ЕГЭ по обществознанию. Самый низкий полученный балл был равен 36, а самый высокий - 75. Выберите утверждения, которые верны при указанных данных.
1) Среди этих выпускников есть человек, который получил 75 баллов за ЕГЭ по обществознанию.
2) Среди этих выпускников есть двадцать два человека с равными баллами за ЕГЭ по обществознанию.
3) Среди этих выпускников есть человек, получивший 20 баллов за ЕГЭ по обществознанию.
4) Баллы за ЕГЭ по обществознанию любого из этих двадцати человек не ниже 35.
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
19. Вычеркните в числе 123456 три цифры так, чтобы получившееся трёхзначное число делилось на 27. В ответе укажите получившееся число.
20. Кузнечик прыгает вдоль координатной прямой в любом направлении на единичный отрезок за прыжок. Сколько существует различных точек на координатной прямой, в которых кузнечик может оказаться, сделав ровно 5 прыжков, начиная прыгать из начала координат?
Ответы:
|
Задание
|
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|
Ответ
|
0,75 | 0,25 | 16 | 12 | −10 | 8 | 9 | 2 | 3241 | 0,75 |
|
Задание
|
11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
|
Ответ
|
2 | 765 | 14,7 | 1432 | 30 | 5 | 1342 | 14; 41 | 135 | 6 |


