ТЕСТ ЕГЭ - 2016 ПО МАТЕМАТИКЕ
ПРОФИЛЬНЫЙ УРОВЕНЬ
ВАРИАНТ 3
Часть 1
1. В пачке 500 листов бумаги формата А4. За неделю в офисе расходуется 1200 листов. Какого наименьшего количества пачек бумаги хватит на 4 недели?
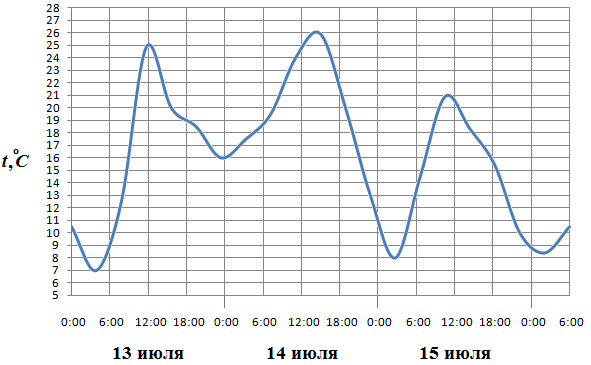
2. На рисунке показано изменение температуры воздуха на протяжении трёх суток. По горизонтали указывается дата и время, по вертикали - значение температуры в градусах Цельсия. Определите по рисунку разность между наибольшей и наименьшей температурой воздуха 15 июля. Ответ дайте в градусах Цельсия.
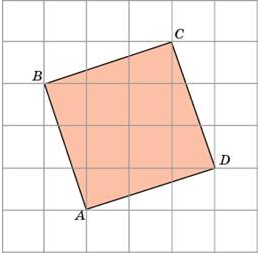
3. Найдите площадь квадрата, изображенного на клетчатой бумаге с размером клетки 1см х 1см (см. рисунок). Ответ дайте в квадратных сантиметрах.
4. Конкурс исполнителей проводится в 5 дней. Всего заявлено 80 выступлений - по одному от каждой страны, участвующей в конкурсе. Исполнитель из России участвует в конкурсе. В первый день запланировано 8 выступлений, остальные распределены поровну между оставшимися днями. Порядок выступлений определяется жеребьёвкой. Какова вероятность, что выступление исполнителя из России состоится в третий день конкурса?
5. Найдите корень уравнения
log5(4 + x) = 2.
6. В треугольнике АВС угол С равен 90°, АС = 4, tg A = 33/4√33. Найдите АВ.
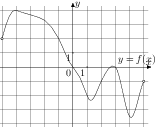
7. На рисунке изображен график функции y = f(x), определённой на интервале (−5; 5). Определите количество целых точек, в которых производная функции отрицательна.
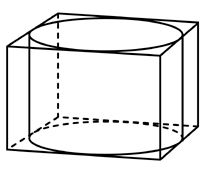
8. Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 4. Объем параллелепипеда равен 16. Найдите высоту цилиндра.
Часть 2
9. Найдите значение выражения
50,36 · 250,32.
10. В боковой стенке высокого цилиндрического бака у самого дна закреплен кран. После его открытия вода начинает вытекать из бака, при этом высота столба воды в нем, выраженная в метрах, меняется по закону
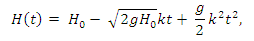
где t - время в секундах, прошедшее с момента открытия крана, Н0 = 20 м - начальная высота столба воды, k = 1/50 - отношение площадей поперечных сечений крана и бака, а g - ускорение свободного падения (считайте g = 10 м/с2). Через сколько секунд после открытия крана в баке останется четверть первоначального объема воды?
11. Два велосипедиста одновременно отправились в 88-километровый пробег. Первый ехал со скоростью, на 3 км/ч большей, чем скорость второго, и прибыл к финишу на 3 часа раньше второго. Найдите скорость велосипедиста, пришедшего к финишу вторым. Ответ дайте в км/ч.
12. Найдите наименьшее значение функции
y = 7sinx − 8x + 9
на отрезке [−3π/2; 0].
13. а) Решите уравнение
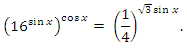
б) Найдите все корни этого уравнения, принадлежащие отрезку [2π; 7π/2].
14. В правильной треугольной пирамиде SABC с вершиной S, все рёбра которой равны 2, точка М - середина ребра АВ, точка О - центр основания пирамиды, точка F делит отрезок SO в отношении 3 : 1, считая от вершины пирамиды.
а) Докажите, что прямая MF перпендикулярна прямой SC.
б) Найдите угол между плоскостью MBF и плоскостью АВС.
15. Решите неравенство
9х−3 − 9х−2 + 9х−1 > 511.
16. Окружность с центром О вписана в угол, равный 60°. Окружность большего радиуса с центром О1 также вписана в этот угол и проходит через точку О.
а) Докажите, что радиус второй окружности вдвое больше радиуса первой.
б) Найдите длину общей хорды этих окружностей, если известно, что радиус первой окружности равен 2√15.
17. 1 января 2015 года Тарас Павлович взял в банке 1,1 млн рублей в кредит. Схема выплаты кредита следующая - 1 числа каждого следующего месяца банк начисляет 2 процента на оставшуюся сумму долга (то есть увеличивает долг на 2%), затем Тарас Павлович переводит в банк платёж. На какое минимальное количество месяцев Тарас Павлович может взять кредит, чтобы ежемесячные выплаты были не более 220 тыс. рублей?
18. При каких а уравнение
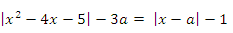
имеет ровно три корня?
19. При каком наибольшем n найдется n семизначных чисел, являющихся последовательными членами одной геометрической прогресии?


