Найдите радиус окружности, вписанной в сектор радиусом 9 и периметром 18 + 3π.

  Дано: сектор, О - центр окружности, вписанной в сектор, АС - радиус сектора, АС = 9, Р_сект = 18 + 3п (см. рисунок).

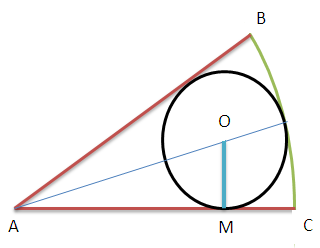
  Найти: радиус окружности.

  Решение: Пусть l_BC - длина дуги ВС; угол ВАС = α. Тогда l_BC = α · AC = α · 9 = 9α.

  Р_сект = АВ + l_BC + АС = 2 · 9 + 9α = 18 + 9α.

  По условию Р_сект = 18 + 3п, значит, 9α = 3п, α = п/3 · угол САО = угол ВАО = α/2 = п/6.

  Пусть r - радиус окружности, вписанной в сектор.

  Из треугольника АОМ: sin OAM = OM/AO;

  sin π/6 =r/(9 − r);

  r/(9 − r) = 1/2;

  r = 3.

  Ответ: 3.