Основания трапеции равны 10 и 5, а диагонали 9 и 12. Найдите площадь трапеции.

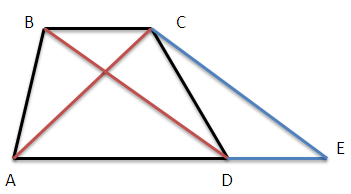
  Дано: ABCD - трапеция, ВС = 5, AD = 10, AC = 9, BD = 12.

  Найти: S_ABCD.

  Решение:

  Через вершину С проведем СЕ параллельно BD (см. рисунок). Продолжим отрезок AD до пересечения с СЕ. Четырехугольник DBCE - параллелограмм, СЕ = BD = 12, DE = BC = 5.

  S_ABCD = S_ACE.

  Найдем S_ACE по формуле Герона. АС = 9, СЕ =12, АЕ = 15.

  Полупериметр треугольника АСЕ p = (9 + 12 + 15)/2 = 18.

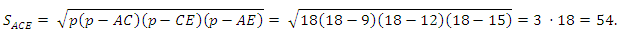
S_ABCD = S_ACE = 54.

  Ответ: 54.