В прямоугольном треугольнике АВС с прямым углом В проведена биссектриса CD. Найдите площадь треугольника ACD, если СВ = 6, BD = 3.

  Решение:

  Так как CD - биссектриса угла АСВ (см. рисунок), то CB/BD = AC/AD = 6/3 = 2/1. Значит, мы можем обозначить АС = 2х; AD = х, х > 0.

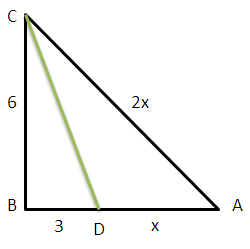
  Из треугольника АВС по теореме Пифагора:

6² + (3 + х)² = (2х)² или х² − 2х − 15 = 0.

  Решениями этого уравнения будут: х₁ = 5; х₂ = −3. Учитывая, что х > 0, получаем х = 5.

S_ΔACD = 1/2 · x · 6 = 15

  Ответ: 15.