В равнобедренном треугольнике АВС с равными сторонами АС и СВ и углом при вершине С, равным 120°, проведены биссектрисы АМ и BN, равные 5. Найдите площадь четырёхугольника ANMB.
Решение:
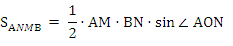
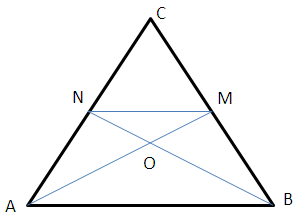
В равнобедренном треугольнике АСВ угол С = 120°, тогда угол А = углу В = 30°. АМ и BN биссектрисы => угол МАВ = углу NBA = 15°, тогда угол AON = 30°.
SANMB = 1/2 · 5 · 1/2 = 1,25
Ответ: 1,25.


