В равнобедренном треугольнике KLM высоты LP и КВ пересекаются в точке О. Найдите площадь треугольника KLO, если LO = 5, PO = 4.

  Решение:

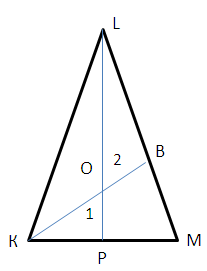
  1) LP = LO + OP (см. рисунок). Получаем, что LP = 5 + 4 = 9.

  2) Δ MLP и Δ OLB - подобны (угол L - общий, угол Р = углу В = 90°), поэтому LP/LB = PM/BO, но РМ = КР; 9/LB = KP/BO, отсюда LB = 9BO/KP.

  3) Δ KOP и Δ LOB - подобны (угол 1 = углу 2 - вертикальные, угол Р = углу В = 90°), следовательно, OP/OB = KP/LB; 4/OB = KP/LB, отсюда LB = (OB · KP)/4.

  4) Из 2) и 3) следует, что 9ВО/КР = (ОВ · КР)/4, отсюда КР² = 36; КР = 6.

  5) S_KLO = S_KLP − S_KOP = 1/2 · KP · LP − 1/2 · KP · OP = 1/2 · 6 · 9 − 1/2 · 6 · 4 = 15.

  Ответ: 15.