В равнобедренном треугольнике длина основания равна 6, а диаметр вписанной окружности равен 2. Найдите радиус описанной около данного треугольника окружности.
Решение:
Пусть в Δ АВС АВ = ВС; АС = 6.
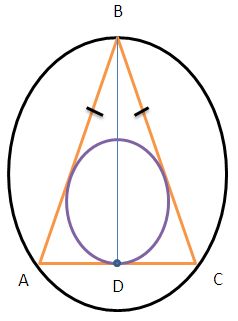
Обозначим через r - радиус вписанной окружности; R - радиус описанной окружности.
Пусть ВС = х, х > 3, тогда
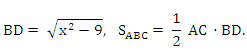
С другой стороны,
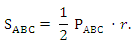
Следовательно, АС · BD = PABC · r;
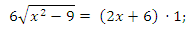
36 · (x2 − 9) = 4x2 + 24x + 36;
32x2 − 24x − 360 = 0;
4x2 − 3x − 45 = 0;
x1 = 3,75
x2 = −3 - не удовлетворяет условию х > 3.
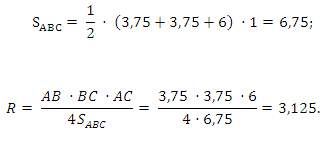
Ответ: 3,125.


