Найдите все пары натуральных чисел а и b, удовлетворяющих равенству
ab + 27 = ab
(в правой части стоит число, получаемое приписыванием десятичной записи числа а перед десятичной записью числа b).
Решение:
Если а = 1, то решений нет. Пусть теперь а > 1.
Разберём сначала случай, когда b - однозначное число. Тогда
ab + 27 = 10a + b;
a(10 − ab − 1) = 27 − b > 0.
При b = 4 получается, что (10 − ab − 1) < 0, а правая часть при однозначных b положительна. Перебираем четыре оставшихся случая. Подходит только b = 2, тогда а = 5. Возможно, что за рассмотрение случая однозначного b, ученик мог получить 2 балла из 4-х. Но ведь мы хотим больше? Тогда идём дальше. Надо показать, что других решений нет. Пусть b ≥ 10.
Пусть а - n-значное число, и b - k-значное. Последовательно получаем:
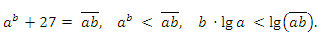
Учитывая, что
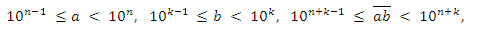
получаем (последовательно усиливая неравенства):
b(n − 1) < n + k.
Теперь группируем:
b(n − 1) < n + k + 1 − 1, (b − 1)(n − 1) < k + 1.
Если число не однозначное, оно заметно превосходит количество знаков своей десятичной записи, другими словами, b > k. Нам хватит оценки b ≥ k + 8.
Получаем (k + 7)(n − 1) < k + 1. Это возможно, только если а - однозначное число. Случай однозначного а надо разобрать отдельно. Для n = 1 наши "усиления" неравенств оказались слишком грубыми. Итак, а - однозначное число, n = 1.
Так как
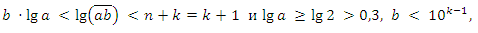
то получаем:
0,3 · 10k − 1 < k + 1,
или
3 · 10k < 100(k + 1).
При k = 2 получаем 300 < 300, неравенство уже не выполняется, не выполнится оно и при k > 2, так как с ростом k левая часть растет намного быстрее, чем правая. Мы показали, что других решений, кроме a = 5, b = 2, нет.
Ответ: a = 5, b = 2.


