Решите уравнение 3^m + 4ⁿ = 5^k в натуральных числах.

  Решение:

  Левая часть уравнения при любых натуральных числах m и n при делении на 3 даёт остаток 1, следовательно, такой же остаток при делении на 3 должен быть и у 5^k, откуда следует, что k - чётное. Пусть k = 2r, r ε N.

  Правая часть уравнения при любом натуральном k при делении на 4 даёт остаток 1, следовательно, такой же остаток при делении на 4 должен быть и у 3^m, откуда следует, что m - чётное. Пусть m = 2s, s ε N.

  Перепишем исходное уравнение в виде

3^2s + 4ⁿ = 5^2r,

или в виде

2²ⁿ = (5^r − 3^s)(5^r + 3^s).

  Тогда 5^r − 3^s = 2^q и 5^r + 3^s = 2^l, где q и l - целые неотрицательные числа и q + l = 2n.

  Таким образом,

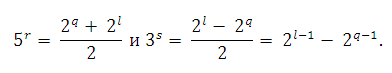
  Число 3^s - нечётное, значит, 2^{l - 1} - 2^{q - 1} нечётно, поэтому q = 1 и 3^s = 2^{l - 1} − 1.

  Следовательно, число l − 1 чётно, l − 1 = 2p (иначе левая часть не делится на 3). Тогда 3^s = (2^p − 1)(2^p + 1) - произведение двух множителей, отличающихся на 2 и являющихся степенями тройки. Ясно, что эти множители 1 и 3, тогда p = 1, s = 1, m = 2s = 2. Далее последовательно получаем:

l = 2p + 1 = 3,

5^r = (2^q + 2^l)/2 = 5,

r = 1,

k = 2r = 2,

q + l = 2n = 4.

  Итак, m = n = k = 2.

  Ответ: m = 2, n = 2, k = 2.