Плоскость делит треугольную пирамиду на два многогранника. Во сколько раз объём большего из многогранников превосходит объём меньшего, если известно, что секущая плоскость делит три ребра, выходящие из одной вершины пирамиды, в отношении 1 : 3, 1 : 4 и 2 : 3, считая от вершины?
Решение:
Рассмотрим треугольную пирамиду ABCD, удовлетворяющую условию (см. рисунок).
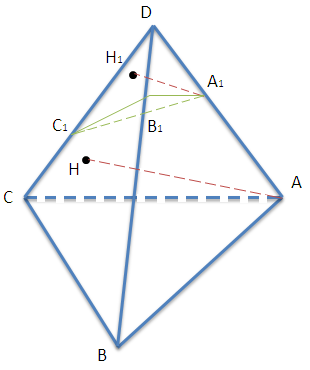
Обозначим через А1, В1 и С1 точки пересечения секущей плоскости с ребрами AD, BD и CD соответственно. Пусть для определенности A1D/A1A = 1/3, B1D/B1B = 1/4, C1D/C1C = 2/3. Обозначим через Н и Н1 основания перпендикуляров, опущенных из точек А и А1 на плоскость BCD. Ясно, что треугольники ADH и A1DH1 подобны. Следовательно,
АН/А1Н1 = AD/A1D = (3 + 1)/1 = 4.
Треугольники BDC и B1DC1 имеют общий угол D, следовательно, их площади относятся как произведения прилежащих к углу сторон:
SΔBDC / SΔB1DC1 = (BD · CD)/(B1D · C1D) = (1+4)(2+3)/1·2 = 25/2.
Имеем:
VABCD = 1/3 · AH · SΔBCD
VA1B1C1D = 1/3 · A1H1 · SΔB1C1D.
Отсюда получаем:
VABCD / VA1B1C1D = 4 · 25/2 = 50.
Таким образом, искомое отношение
(VABCD − VA1B1C1D) / VA1B1C1D = VABCD / VA1B1C1D − 1 = 49.
Ответ: 49.


