В правильной треугольной пирамиде DABC сторона основания равна 6√3, а высота DH пирамиды, опущенная из вершины D на плоскость основания АВС, равна 4. Найдите расстояние от точки D до плоскости, проходящей через точку Н параллельно плоскости DBC.

  Решение:

  Построим сечение пирамиды плоскостью, проходящей через точку Н параллельно плоскости DBC (см. рисунок).

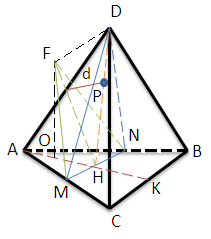
Для этого через точку Н проведем MN параллельно ВС. Через точку М проведем MF параллельно CD. Сечение MFN - искомое. Пусть d - расстояние от точки D до плоскости MFN.

  1) В треугольнике АВС проведем высоту АК;

АК = АС · sin 60° = (6√3 · √3)/2 = 9.

  Так как пирамида DABC - правильная, то Н является в треугольнике АВС точкой пересечения медиан. Следовательно, АН = 2/3 · АК = 2/3 · 9 = 6.

  2) Треугольник САВ подобен треугольнику MAN с коэффициентом подобия k = 2/3. Тогда МС = 1/3 · АС, MN = 2/3 · BC = 2/3 · 6√3 = 4√3.

  Треугольник CAD подобен треугольнику MAF с коэффициентом подобия k = 2/3. Следовательно, FD = 1/3 · AD. Проведем FO параллельно DH, О принадлежит АВС. Тогда треугольник HAD подобен треугольнику OAF с коэффициентом подобия k = 2/3, следовательно, ОН = 1/3 · АН = 6 · 1/3 = 2, OF = 2/3 · DH = 8/3.

  3) Так как DH перпендикулярна АВС, то OF перпендикулярен АВС, следовательно, OF перпендикулярен АН. Из треугольника FOH:

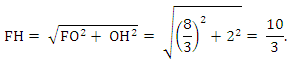
  4) Проведем FP параллельно АН, АН перпендикулярен MDN, значит, FP перпендикулярен MDN, следовательно, FP - высота пирамиды FMND.

  5) Рассмотрим пирамиду DFMN:

V = 1/3 · S_FMN · d, с другой стороны,

V = 1/3 · S_MDN · FP, FP = OH =2,

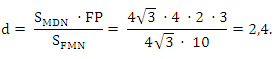
  Ответ: 2,4.