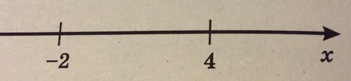ЛИНЕЙНЫЕ УРАВНЕНИЯ И УРАВНЕНИЯ, ПРИВОДИМЫЕ К ЛИНЕЙНЫМ
РЕШЕНИЕ ЗАДАЧ С ПАРАМЕТРАМИ
1. Решите уравнение: 2а(а − 2)х = а − 2.
Решение: Здесь контрольными будут те значения параметра, при которых коэффициент при х обращается в ноль. Такими значениями являются: а = 0 и а = 2. Эти значения разбивают множество значений параметра на три подмножества:
1) а = 0;
2) а = 2;
3) а ≠ 0, а ≠ 2.
Рассмотрим эти случаи.
1) При а = 0 уравнение принимает вид 0 · х = −2. Это уравнение не имеет корней.
2) При а = 2 уравнение принимает вид 0 · х = 0. Корнем этого уравнения является любое действительное число.
3) При а ≠ 0 и а ≠ 2 из уравнения получаем:
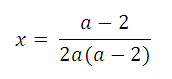
откуда
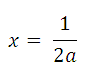
Ответ:
1) если а = 0, то корней нет;
2) если а = 2, то х - любое действительное число;
3) если
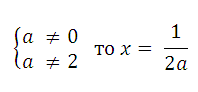
2. Решите уравнение: (а2 − 2а + 1) · х = а2 + 2а − 3.
Решение: Находим контрольные значения параметра а: а2 − 2а + 1 = 0, а = 1.
Множество значений параметра разбивается на два подмножества:
1) а = 1;
2) а ≠ 1.
Решим уравнение на каждом из них.
1) а = 1; 0 · х = 0, х ε R.
2) а ≠ 1;
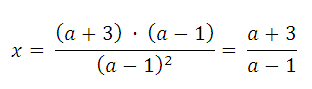
Ответ:
1) если а = 1, то х ε (−∞; +∞);
2) если а ≠ 1, то х = (а + 3) ÷ (а − 1).
3. Решите уравнение:
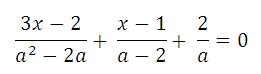
Решение: Освободимся от знаменателя в уравнении, для этого умножим обе его части на а(а − 2) ≠ 0.
3а − 2 + ах − а + 2а − 4 = 0
х(3 + а) = 6 − а
Контрольными значениями будут: а = 0, а = 2, а = −3.
Рассмотрим решение уравнения на подмножествах:
1) а = 0;
2) а = 2;
3) а = −3;
4)
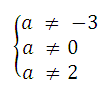
Итак:
1) а = 0. Уравнение не имеет решений.
2) а = 2. Уравнение не имеет решений.
3) а = −3. х·0 = 6 + 3 = 9, х ε Ø.
4)
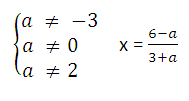
Ответ: Ø при а = −3, а = 0, а = 2;
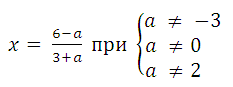
4. При всех значениях параметра а решите уравнение:
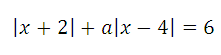
Решение: Разобьем числовую прямую на ряд промежутков нулями: х = −2, х = 4 и рассмотрим решение уравнения на каждом из них.
1) х < −2;
2) −2 ≤ х < 4
3) х ≥ 4
Итак:
1) х < −2.
−х − 2 − ах + 4а = 6
х(а + 1) = 4а − 8
а) а + 1 = 0, а = −1, 0 · х = −12; нет решений.
б) а + 1 ≠ 0, а ≠ −1,
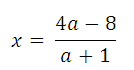
Поскольку х < −2, то
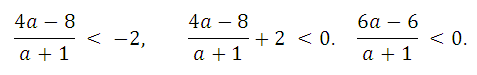
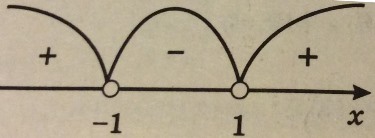
Решим полученное неравенство методом интервалов.
Его решение: −1 < а < 1.
Итак, при −1 < а < 1
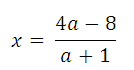
2) −2 ≤ х ≤ 4, х + 2 − ах + 4а = 6, х(1 − а) = 4 − 4а.
а) Если а = 1, то х · 0 = 0; х - любое действительное число, но так как −2 ≤ х ≤ 4, то при а = 1 −2 ≤ х ≤ 4.
б) Если а ≠ 1, то х = 4(1 − а) ÷ (1 − а) = 4.
3) х ≥ 4.
х + 2 + ах − 4а = 6
х(а + 1) = 4 + 4а
а) а + 1 = 0, а = −1, х · 0 = 0, х - любое. Поскольку х ≥ 4, то при а = −1 х ≥ 4.
б) а + 1 ≠ 0, а ≠ −1, х = 4.
Ответ:
х = 4 при а < −1;
х ≥ 4 при а = −1;
х1 = 4, х2 = (4а − 8) ÷ (а + 1) при −1 < а < 1;
−2 ≤ х ≤ 4 при а = 1;
х = 4 при а > 1.