Сплавляя два одинаковых по весу куска чугуна с разным содержанием хрома, получили сплав, в котором содержится 12 кг хрома. Найдите процентное содержание хрома в полученном сплаве, если известно, что содержание хрома в первом куске чугуна было на 5% меньше, чем во втором, и что если бы первый кусок был в два раза тяжелее, то в сплаве оказалось бы 16 кг хрома.

РЕШЕНИЕ:

  Обозначим через х и у процентное содержание хрома соответственно в первом и втором куске чугуна, через Р вес каждого из кусков чугуна. Тогда в первом куске чугуна содержалось (Р · (х ÷ 100)) кг хрома, а во втором - (Р · (у ÷ 100)) кг хрома. Так как в полученном сплаве оказалось 12 кг хрома, то выполняется равенство:

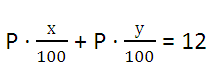
  Если бы первый кусок чугуна весил 2Р кг, то в сплаве содержалось бы ((2Р · х/100) + (Р · у/100)) кг хрома, что, по условию, равняется 16 кг. Учитывая также, что содержание хрома в первом куске чугуна было на 5% меньше, чем во втором, получаем систему уравнений:

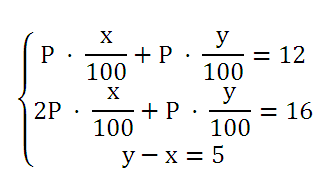
  Разделим первое уравнение системы на второе и, воспользовавшись третьим уравнением, в полученное равенство подставим у = х + 5. В результате таких действий будем иметь:

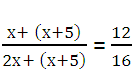
(2х + 5) ÷ (3х + 5) = 3/4

4(2х + 5) = 3(3х + 5)

х = 5

Значит, у = 10.

  Значение Р найдем из первого уравнения системы:

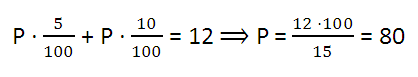
  Итак, полученный из двух одинаковых по весу кусков чугуна сплав весит 160 кг и содержит 12 кг хрома. Следовательно, процентное содержание хрома в таком сплаве равно (12 ÷ 160) · 100 = 7,5 (%).

  Ответ: 7,5.