ТЕСТ ЕГЭ - 2015 ПО МАТЕМАТИКЕ
ПРОФИЛЬНЫЙ УРОВЕНЬ
ВАРИАНТ 5
Тест предназначен для решения в ходе подготовки к ЕГЭ - 2015 по математике. Структура теста и сложность включенных в него заданий соответствуют демонстрационному варианту ЕГЭ - 2015 по математике, опубликованному на официальном сайте ФИПИ. Вероятность попадания данных заданий в реальные варианты экзаменационных работ не высока, однако, овладев навыками по их решению, Вы будете готовы и к решению экзаменационного варианта.
ЧАСТЬ 1
1. Для ремонта квартиры купили 42 рулона обоев. Сколько пачек обойного клея нужно купить, если одна пачка клея рассчитана на 8 рулонов?
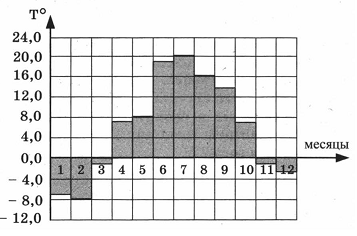
2. На диаграмме показана среднемесячная температура воздуха в Санкт-Петербурге за каждый месяц 1999 года. По горизонтали указываются месяцы, по вертикали - температура в градусах Цельсия. Определите по диаграмме, сколько месяцев второго полугодия 1999 года средняя температура была ниже 14 °С.
3. Керамическая плитка одной и той же торговой марки выпускается трёх разных размеров. Плитки упакованы в пачки. Пользуясь данными таблицы, определите, в каком случае цена одного квадратного метра плитки будет наименьшей. В ответ запишите найденную наименьшую цену квадратного метра в рублях.
| Размер плитки (см) | Количество плиток в пачке | Цена пачки |
| 20 х 30 | 20 | 612 р. |
| 30 х 40 | 11 | 679 р. 80 к. |
| 20 х 20 | 29 | 585 р. 80 к. |
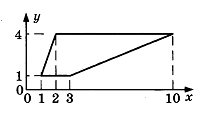
4. Найдите площадь трапеции, изображённой на рисунке.
5. В случайном эксперименте бросают две игральные кости (кубика). Найдите вероятность того, что в сумме выпадет 7 очков. Результат округлите до сотых.
6. Решите уравнение
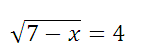
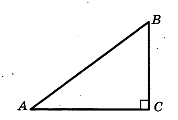
7. В треугольнике АВС угол С равен 90°, cos A = 4/5. Найдите sin B.
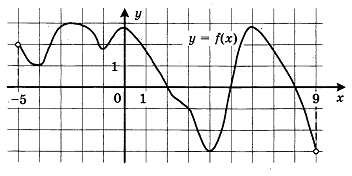
8. На рисунке изображён график функции y = f(x), определённой на интервале (−5; 9). Найдите количество точек, в которых производная функции f(x) равна 0.
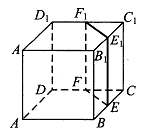
9. В кубе ABCDA1B1C1D1 точки Е, F, E1 и F1 являются серединами рёбер BC, DC, B1C1 и D1C1 соответственно. Объём призмы, отсекаемой от куба плоскостью EFF1, равен 21. Найдите объём куба.
ЧАСТЬ 2
10. Найдите значение выражения
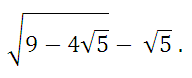
11. Ёмкость высоковольтного конденсатора в телевизоре С = 3 · 10-6 Ф. Параллельно с конденсатором подключён резистор с сопротивлением R = 5 · 106 Ом. Во время работы телевизора напряжение на конденсаторе U0 = 9 кВ. После выключения телевизора напряжение на конденсаторе убывает до значения U (кВ) за время, определяемое выражением
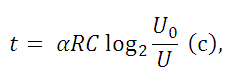
где α = 1,1 - постоянная.
Определите наибольшее возможное напряжение на конденсаторе, если после выключения телевизора прошло не менее 33 секунд. Ответ дайте в кВ (киловольтах).
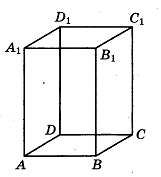
12. Диагональ правильной четырёхугольной призмы наклонена к плоскости основания под углом 30°. Боковое ребро равно 3. Найдите диагональ призмы.
13. Первая труба наполняет бак объёмом 600 литров, а вторая труба - бак объёмом 900 литров. Известно, что одна из труб пропускает в минуту на 3 л воды больше, чем другая. Сколько литров воды в минуту пропускает вторая труба, если баки были наполнены за одно и то же время?
14. Найдите наибольшее значение функции
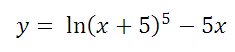
на отрезке [−4,5; 0].
15. а) Решите уравнение
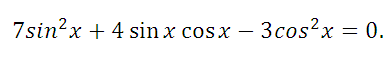
б) Укажите корни, принадлежащие отрезку
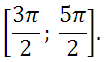
16. Диаметр окружности основания цилиндра равен 26, образующая цилиндра равна 21. Плоскость пересекает его основания по хордам длины 24 и 10. Расстояние между этими хордами равно
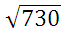
а) Постройте прямую пересечения этой плоскости с плоскостью, проходящей через диаметры оснований, перпендикулярные этим хордам.
б) Найдите угол между этой плоскостью и плоскостью основания цилиндра.
17. Решите неравенство
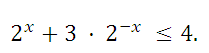
18. На катетах АС и ВС прямоугольного треугольника АВС вне треугольника построены квадраты ACDE и BFKC. Точка М - середина гипотенузы АВ, Н - точка пересечения прямых CM и DK.
а) Докажите, что
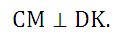
б) Найдите МН, если известно, что катеты треугольника АВС равны 30 и 40.
19. Степан хочет взять в кредит 1,2 млн рублей. Погашение кредита происходит раз в год равными суммами (кроме, может быть, последней) после начисления процентов. Ставка процента 10% годовых. На какое минимальное количество лет может Степан взять кредит, чтобы ежегодные выплаты были не более 290 тысяч рублей?
20. Найдите все значения а, при каждом из которых уравнение
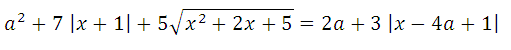
имеет хотя бы один корень.
21. Имеется 8 карточек. На них записывают по одному каждое из чисел −1, 2, 4, −6, 7, −8, −10, 12. После этого числа на каждой карточке складывают, а полученные восемь сумм перемножают.
а) Может ли в результате получиться 0?
б) Может ли в результате получиться 1?
в) Какое наименьшее целое неотрицательное число может в результате получиться?


